안녕하세요

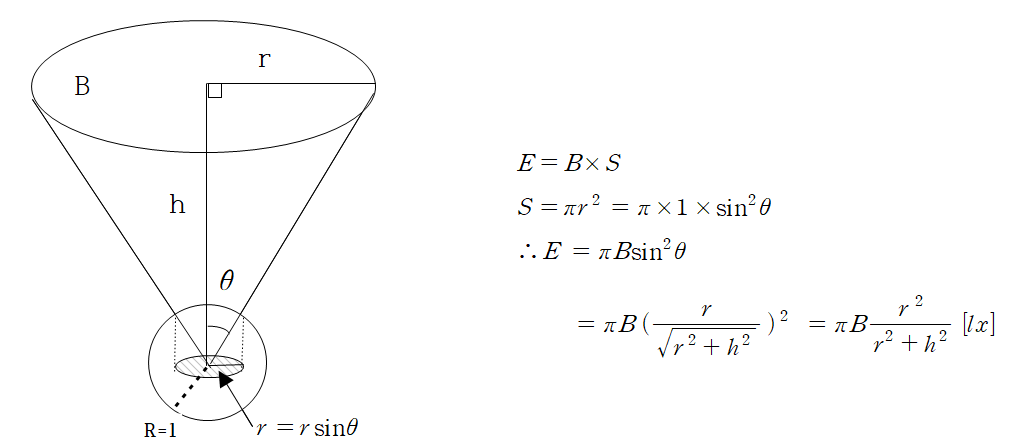
광원의 크기가 존재하는 경우 (중심으로 향하는 조도 계산)은 일반조도 계산법 하고는 다르게 해석 합니다

광원의 크기가 존재하는 경우 (중심으로 향하는 조도 계산)은 단위구법 또는 추면적분법, 등조도법을 활용하게 되는데 여기서는 단위구법을 이용한 조도계산을 말하게 됩니다.

단위구법은 조도계산 E=B(휘도) X S(피조면의 면적)으로 계산됩니다.

이때 면적 S는 빛을 받는 부분 즉 원의 면적이 됨으로 파이 X (R)반지름의 제곱이 됩니다.  그림의 아래부분 빛을 받는쪽을 보시면

면적 계산이 문제가 될수 있는데 우리는 단위구법을 적용함으로 반지름이 1인구를 그리게 됩니다. 

다음 그림을 참조해 주세요 사선 친 부분이 실제 빛을 받는 부분이 됩니다. 실제 빛을 받는 반지름은 1 X 사인제곱이 되는것입니다.

그래서 E=파이 X B X 사인제곱세타 가 되는것입니다.  여기서 사인값을 구해서 넣게 되면 반구형 천정에 조도 계산식이 완성됩니다.

수고하시구요  열공하세요